COW arm: Difference between revisions
No edit summary |
|||
| Line 19: | Line 19: | ||
We can do this with a concept called inverse kinematics. Inverse kinematics can tell us the angles of the arm joints that we need to get to any given points. This is a much harder process than forward kinematics, which is what we do if we have the angles of the arm and want to see where it will end up. Inverse kinematics can involve a lot of fancy and complicated math, with linear algebra and matrices involved, but for a simpler arm like mine, we can just use concepts from geometry and trig functions. Actually, we don't even need to do that, because a 2 link arm like mine is usually the first or second example in the book if you happen to search up "inverse kinematics" on Google. The derivation comes from law of sines and cosines, but at the end of the day we end up with the following formulas: | We can do this with a concept called inverse kinematics. Inverse kinematics can tell us the angles of the arm joints that we need to get to any given points. This is a much harder process than forward kinematics, which is what we do if we have the angles of the arm and want to see where it will end up. Inverse kinematics can involve a lot of fancy and complicated math, with linear algebra and matrices involved, but for a simpler arm like mine, we can just use concepts from geometry and trig functions. Actually, we don't even need to do that, because a 2 link arm like mine is usually the first or second example in the book if you happen to search up "inverse kinematics" on Google. The derivation comes from law of sines and cosines, but at the end of the day we end up with the following formulas: | ||
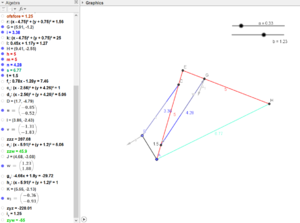
[[File:Cow-invknm-v1.png|thumb|Verifying the inverse kinematics with the geogebra geometry model we made earlier.]] | |||
<pre> | |||
q1 = pi-acos((x^2+y^2-a1^2-a2^2)/(2*a1*a2)); | |||
q2 = atan(y/x) + atan((a2*sin(-q1-pi))/(a1+a2*cos(-q1-pi))); | |||
</pre> | |||
where '''q1''' and '''q2''' are the angles shown on the GeoGebra model. We also have the other parameters of the arm, like the lengths of the arm segments('''a'''), and the lengths along the arm where the actuators are mounted ('''l''' and '''m'''). Variables with a '''2''' after them are for the arm section, and ones with a '''1''' are for the forearm section. | |||
Revision as of 17:51, 11 August 2019
For this year's Winter Camp, Space is the theme. Therefore, after upgrading my electric wheelchair robot base this spring with a new motor controller, I decided that it should also have a robotic arm, making it useful as a Mars rover - esque robot platform. The wheelchair base weights a hefty 100+ pounds, and I want this arm to be actually useful (ie, able to lift more than a tissue box). I have named it the Cow arm, as it is designed to be beefier than those crummy kit arms that use servos.
Upper and Lower Arm
I designed this arm after seeing this Hackaday.io project which uses linear actuators to provide forces along the length of the arm, much like the muscles in our own arm. Many arm designs I have seen use very high torque gearmotors in the arm joints to provide torque on the arm, but I don't have the ability to make one and they are astronomically expensive. Meanwhile, these linear actuators cost just 10s of dollars. I picked up a couple for testing, and if they work, they should take care of the largest force sections of the arm straight away.
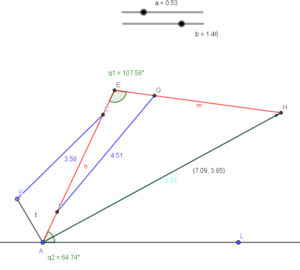
I also began to design the geometry of the arm; for this I have used a free program called GeoGebra, which I had remembered from a class I took. This program is essentially the electronic version of a paper, compass and straightedge. More importantly, objects can be changed - for example, I can change the diameter of a circle - and the rest of the lines will instantly update themselves to the new position. I can even attach the size of a circle to a slider, and drag it around to see what changing the size does in real time. It doesn't have all the constraint features of a CAD package, but the dynamic updating ability is really powerful.
I constructed the basic arm design I wanted to use, and then adjusted the joints of the linear actuators of the arm around until I got the range of the arm about how I wanted. Also, GeoGebra supports vectors, so by using the maximum force listed by the linear actuators and some vector projection, I could estimate the max force I might expect to pick up at the end of the arm. Obviously, this varies depending on how far the arm is extended, just like our own arms. Neglecting the weight of the arm itself, I was quite impressed to realize the arm might be able to pick up 10-30 pounds quite easily.
At present, the arm design looks more like a crane or backhoe than an arm. GeoGebra files for this design: File:Cow-arm-lower-upper-v3-ggb.zip
Encoders
Software/The Math
There's one big difference between the arm I just designed and the one attached onto my shoulder - how do you control it? When we want to pick something up, we don't think about how our muscles need to move, we just move our arm towards the object. With this arm, ideally I don't want to manually control it by moving each actuator. I should be able to just specify a location, and the arm should go there.
We can do this with a concept called inverse kinematics. Inverse kinematics can tell us the angles of the arm joints that we need to get to any given points. This is a much harder process than forward kinematics, which is what we do if we have the angles of the arm and want to see where it will end up. Inverse kinematics can involve a lot of fancy and complicated math, with linear algebra and matrices involved, but for a simpler arm like mine, we can just use concepts from geometry and trig functions. Actually, we don't even need to do that, because a 2 link arm like mine is usually the first or second example in the book if you happen to search up "inverse kinematics" on Google. The derivation comes from law of sines and cosines, but at the end of the day we end up with the following formulas:
q1 = pi-acos((x^2+y^2-a1^2-a2^2)/(2*a1*a2)); q2 = atan(y/x) + atan((a2*sin(-q1-pi))/(a1+a2*cos(-q1-pi)));
where q1 and q2 are the angles shown on the GeoGebra model. We also have the other parameters of the arm, like the lengths of the arm segments(a), and the lengths along the arm where the actuators are mounted (l and m). Variables with a 2 after them are for the arm section, and ones with a 1 are for the forearm section.